Recently, on a Russian Telegram channel, it was claimed that using solar data and comparing to the angle of shadows in the pictures, a definite date can be placed on the second satellite image, and that it is not 19. March, but 1. April. (Some arguments about satellite flight paths are also made - it seems they may have confused timezones and believe that the satellite has to be directly over Bucha to get imagery, as well as claims about sand being washed off the road, which I cannot see at all in the images, so I'm not addressing.) An English summary is made here on Russian Pravda for those interested. Satellite images are taken from the New York Times, they are copyright Maxar.

I am not entirely sure what precisely they did. They point to the elevation of the sun above the horizon (altitude) as being crucial, but why they've decided it has to be 42°, I don't know, and they give no explanation.

The solar azimuth (if you imagine a compass at a given location, it is the number of degrees from North where the sun is shining from) is important, as this determines the time of day. The solar elevation determines the length of shadows that are cast, and for a given time of day, will change throughout the year (increasing from beginning of winter to beginning of summer).

The shadows cast overlay each other, although in the later image, they are shorter, but it indicates the same azimuth, so the same time of day (leaving off DST). First order of business is to determine the azimuth. The only tool I am using is the free image manipulation program GIMP. I took an image of the street map from Google Maps. By default, the top of the image is true north. Using the measure tool in GIMP, I determined Yablonska Street (Vul. Yablunsʹka) runs 25° above the west. Then the satellite image of the street can be tilted by that much in GIMP, and one of the shadows of a powerline pole measured to determine the asimuth of the sun, 165°

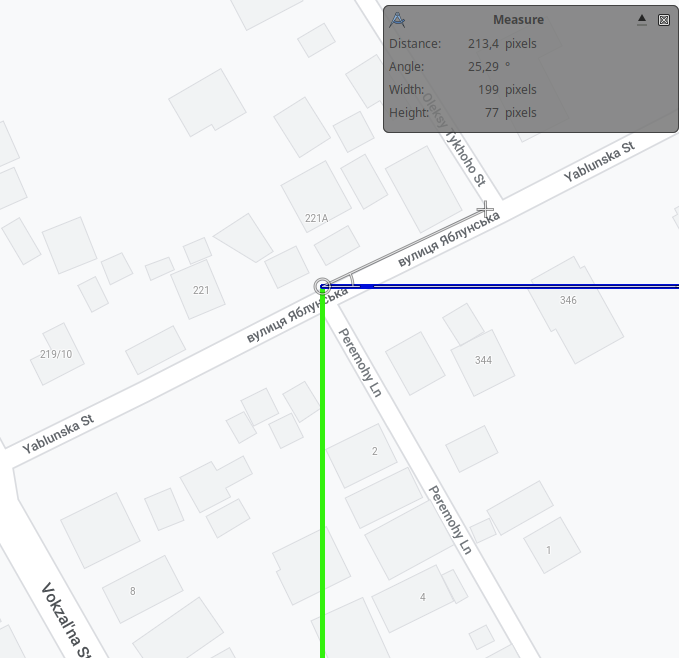
Looking at the different powerline poles, the one on the corner of Yablunska St. and Peremohy Ln. appears to be visible as a light dot in the position where it is visible on Google Street View. Using the Gimp measurement tool, the length (in pixels) of the shadows on the two images can be determined.

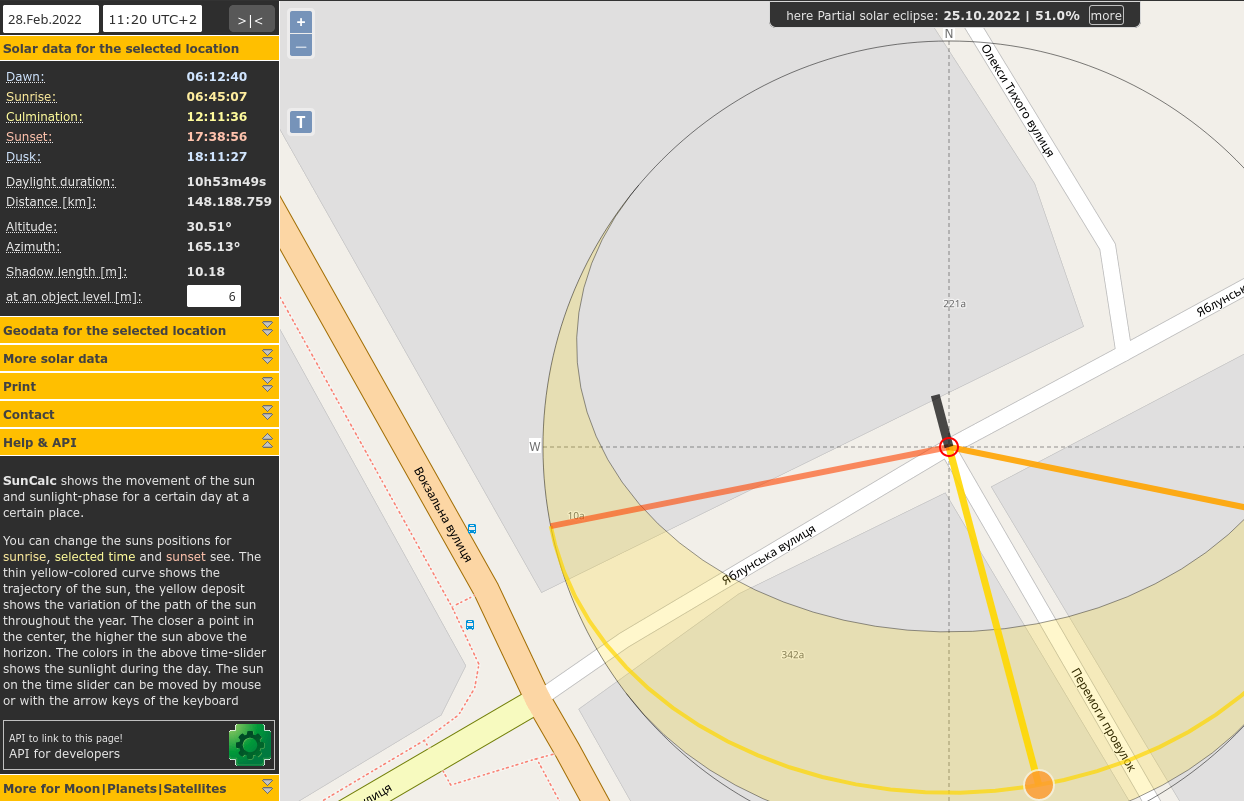
Knowing the azimuth, Suncalc.org can be used to find the time (i.e. by putting in different times and narrowing done on the azimuth angle till it is 165°). Suncalc calculates shadow length for a given height. All the matters is comparing ratios, but anyway, I put in a guess that a power pole is 6m high. Would be interesting to know how high this particularly pole is, and if anyone reading this lives in Bucha (or works for electrical distribution company there), would be glad to know. So then go through and find the heights on the dates 28. Feb, 19. Mar, and 1. Apr (bearing in mind on the last date the time needs to be shifted by an hour to account for DST), respectively, these are 10.18m, 7.68m and 6.39m. 206px/270px = 0.76 If the second image is truly on 19. March, then the ratio of lengths should be 7.68m/10.18m = 0.75, while if it were 1. Apr is would be 6.39m/10.18m=0.62. So which date looks more likely to you?